你可能听说过函数式编程(Functional programming),甚至已经使用了一段时间。
但是,你能说清楚,它到底是什么吗?

网上搜索一下,你会轻松找到好多答案。
与面向对象编程(Object-oriented programming)和过程式编程(Procedural programming)并列的编程范式。
最主要的特征是,函数是第一等公民。
强调将计算过程分解成可复用的函数,典型例子就是
map方法和reduce方法组合而成 MapReduce 算法。
上面这些说法都对,但还不够,都没有回答下面这个更深层的问题。

为什么要这样做?
这就是,本文要解答的问题。我会通过最简单的语言,帮你理解函数式编程,并且学会它那些基本写法。
需要声明的是,我不是专家,而是一个初学者,最近两年才真正开始学习函数式编程。一直苦于看不懂各种资料,立志要写一篇清晰易懂的教程。下面的内容肯定不够严密,甚至可能包含错误,但是我发现,像下面这样解释,初学者最容易懂。
另外,本文比较长,阅读时请保持耐心。结尾还有 Udacity 的《前端工程师认证课程》的推广,非常感谢他们对本文的赞助。
一、范畴论
函数式编程的起源,是一门叫做范畴论(Category Theory)的数学分支。

理解函数式编程的关键,就是理解范畴论。它是一门很复杂的数学,认为世界上所有的概念体系,都可以抽象成一个个的"范畴"(category)。
1.1 范畴的概念
什么是范畴呢?
维基百科的一句话定义如下。
"范畴就是使用箭头连接的物体。"(In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". )
也就是说,彼此之间存在某种关系的概念、事物、对象等等,都构成"范畴"。随便什么东西,只要能找出它们之间的关系,就能定义一个"范畴"。
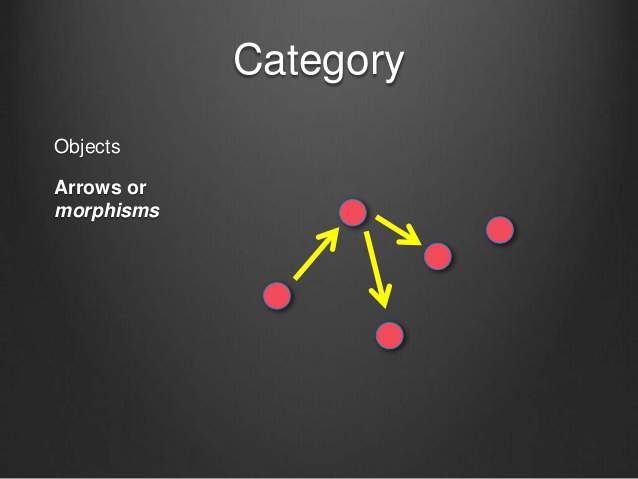
上图中,各个点与它们之间的箭头,就构成一个范畴。
箭头表示范畴成员之间的关系,正式的名称叫做"态射"(morphism)。范畴论认为,同一个范畴的所有成员,就是不同状态的"变形"(transformation)。通过"态射",一个成员可以变形成另一个成员。
1.2 数学模型
既然"范畴"是满足某种变形关系的所有对象,就可以总结出它的数学模型。
所有成员是一个集合
变形关系是函数
也就是说,范畴论是集合论更上层的抽象,简单的理解就是"集合 + 函数"。
理论上通过函数,就可以从范畴的一个成员,算出其他所有成员。
1.3 范畴与容器
我们可以把"范畴"想象成是一个容器,里面包含两样东西。
值(value)
值的变形关系,也就是函数。
下面我们使用代码,定义一个简单的范畴。
class Category{constructor(val){ this.val = val;}addOne(x){return x +1;}}
上面代码中,Category是一个类,也是一个容器,里面包含一个值(this.val)和一种变形关系(addOne)。你可能已经看出来了,这里的范畴,就是所有彼此之间相差1的数字。
注意,本文后面的部分,凡是提到"容器"的地方,全部都是指"范畴"。
1.4 范畴论与函数式编程的关系
范畴论使用函数,表达范畴之间的关系。
伴随着范畴论的发展,就发展出一整套函数的运算方法。这套方法起初只用于数学运算,后来有人将它在计算机上实现了,就变成了今天的"函数式编程"。
本质上,函数式编程只是范畴论的运算方法,跟数理逻辑、微积分、行列式是同一类东西,都是数学方法,只是碰巧它能用来写程序。
所以,你明白了吗,为什么函数式编程要求函数必须是纯的,不能有副作用?因为它是一种数学运算,原始目的就是求值,不做其他事情,否则就无法满足函数运算法则了。
总之,在函数式编程中,函数就是一个管道(pipe)。这头进去一个值,那头就会出来一个新的值,没有其他作用。
二、函数的合成与柯里化
函数式编程有两个最基本的运算:合成和柯里化。
2.1 函数的合成
如果一个值要经过多个函数,才能变成另外一个值,就可以把所有中间步骤合并成一个函数,这叫做"函数的合成"(compose)。
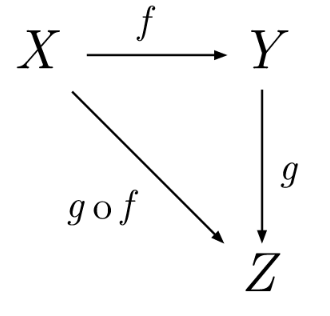
上图中,X和Y之间的变形关系是函数f,Y和Z之间的变形关系是函数g,那么X和Z之间的关系,就是g和f的合成函数g·f。
下面就是代码实现了,我使用的是 JavaScript 语言。注意,本文所有示例代码都是简化过的,完整的 Demo 请看《参考链接》部分。
合成两个函数的简单代码如下。
const compose =function(f, g){returnfunction(x){returnf(g(x));};}
函数的合成还必须满足结合律。
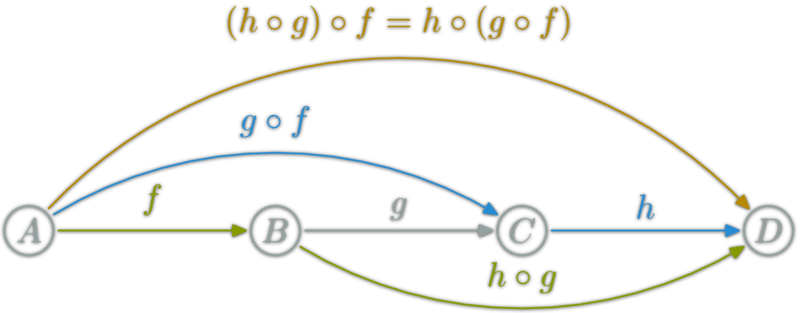
compose(f,compose(g, h))// 等同于compose(compose(f, g), h)// 等同于compose(f, g, h)
合成也是函数必须是纯的一个原因。因为一个不纯的函数,怎么跟其他函数合成?怎么保证各种合成以后,它会达到预期的行为?
前面说过,函数就像数据的管道(pipe)。那么,函数合成就是将这些管道连了起来,让数据一口气从多个管道中穿过。
2.2 柯里化
f(x)和g(x)合成为f(g(x)),有一个隐藏的前提,就是f和g都只能接受一个参数。如果可以接受多个参数,比如f(x, y)和g(a, b, c),函数合成就非常麻烦。
这时就需要函数柯里化了。所谓"柯里化",就是把一个多参数的函数,转化为单参数函数。
// 柯里化之前functionadd(x, y){return x + y;}add(1,2) // 3// 柯里化之后functionaddX(y){returnfunction(x){return x + y;};}addX(2)(1) // 3
有了柯里化以后,我们就能做到,所有函数只接受一个参数。后文的内容除非另有说明,都默认函数只有一个参数,就是所要处理的那个值。
三、函子
函数不仅可以用于同一个范畴之中值的转换,还可以用于将一个范畴转成另一个范畴。这就涉及到了函子(Functor)。
3.1 函子的概念
函子是函数式编程里面最重要的数据类型,也是基本的运算单位和功能单位。
它首先是一种范畴,也就是说,是一个容器,包含了值和变形关系。比较特殊的是,它的变形关系可以依次作用于每一个值,将当前容器变形成另一个容器。
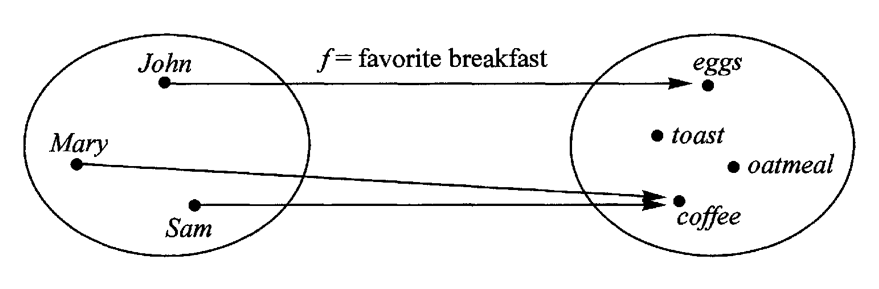
上图中,左侧的圆圈就是一个函子,表示人名的范畴。外部传入函数f,会转成右边表示早餐的范畴。
下面是一张更一般的图。
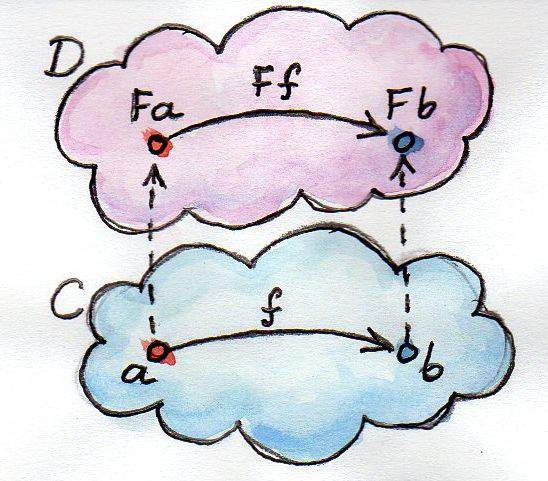
上图中,函数f完成值的转换(a到b),将它传入函子,就可以实现范畴的转换(Fa到Fb)。
3.2 函子的代码实现
任何具有map方法的数据结构,都可以当作函子的实现。
class Functor{constructor(val){ this.val = val;}map(f){returnnewFunctor(f(this.val));}}
上面代码中,Functor是一个函子,它的map方法接受函数f作为参数,然后返回一个新的函子,里面包含的值是被f处理过的(f(this.val))。
一般约定,函子的标志就是容器具有map方法。该方法将容器里面的每一个值,映射到另一个容器。
下面是一些用法的示例。
(newFunctor(2)).map(function(two){return two +2;});// Functor(4)(newFunctor('flamethrowers')).map(function(s){return s.toUpperCase();}
