堆排序（heapsort）是一种比较快速的排序方式，它的时间复杂度为O(nlgn)，而且堆排序具有空间原址性：即任何时候只需要有限（常数个）的空间来存储临时数据。而且堆排序还被应用在构造优先级队列中，本文将会用Java实现一个最大堆，并利用最大堆实现优先级队列。

最大堆的性质

1.是一棵近似的完全二叉树，除了最底层，其它是全满，且从左向右填充。 
2.树的每个节点对应数组一个元素，根节点对应数组下标0元素。 
3.对于下标i，它的父节点下标为(i + 1) / 2 - 1，左孩子节点下标为i * 2 + 1，右孩子节点下标为i * 2 + 2。 
4.最大堆中，每个结点都必须大于等于左右孩子节点。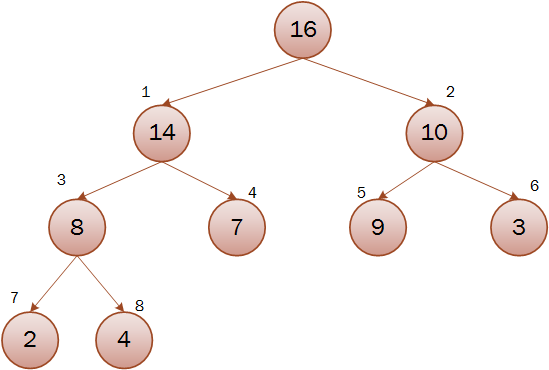 


堆排序

1.维护最大堆 
为了建立一个最大堆，我们需要设计一个算法来维护最大堆的性质。对于节点i，我们假设它们的左右子树都是最大堆，而节点i因为小于左右孩子而违背了最大堆的性质，因此我们需要对节点i进行逐级下降，从而使得以节点i为根结点的子树满足最大堆的性质。

private void maxHeapify(int[] a, int i, intlength) {    int l = left(i);    int r = right(i);    intmax;        if (l < length && a[l] > a[i]) {        max = l;    } else {        max = i;    }    if (r < length && a[r] > a[max]) {        max = r;    }    if (max != i) {        swap(a, i, max);        maxHeapify(a, max, length);    }  }

上述代码的解释是： 
对于节点i（即数组下标i）,首先获取它的左右子孩子下标，分别存储到l，r变量中，其中left和right函数可以根据最大堆的性质得到，如下：

privateintleft(int i) {        return i * 2 + 1;    }    privateintright(int i) {        return i * 2 + 2;    }

变量length是要维护的数组的长度，它的值<=数组的真实长度。临时变量max用来存储节点i，左孩子和右孩子这三者最大者的下标。因此，首先比较左孩子a[l]是否大于节点i，是的话将左孩子下标l赋值给max，否则，当前最大者仍为节点i，并把i的值赋给max。然后当前最大者和右孩子比较，小于右孩子的话就把下标r赋值给max。到目前为止，我们找到了节点i，左孩子和右孩子这三者之中的最大者的下标max，如果节点i本来就是最大的，那么就不需要维护了，所以函数结束。否则的话，有孩子节点大于节点i，因此我们需要将节点i和较大的那个孩子进行交换，即swap(a, i, max)，swap函数如下：

privatevoidswap(int[] a, int i, int j) {        int tmp = a[i];        a[i] = a[j];        a[j] = tmp;    }

交换之后，节点max的值变成了较小的原来节点i的值，因此，以节点max为根节点的子树可能违背最大堆的性质。注意到此时问题和一开始一模一样，只是节点i变成了节点max，因此递归调用maxHeapify(a, max, length)即可。

如果把第一张图的节点1的值改为1，这时从节点1开始调用maxHeapify(a, 1, a.length，整个流程如下：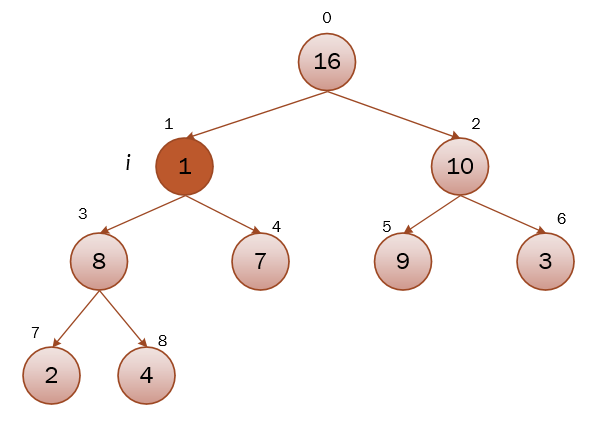 



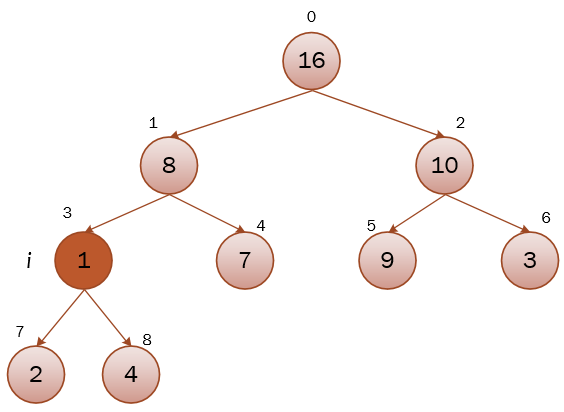
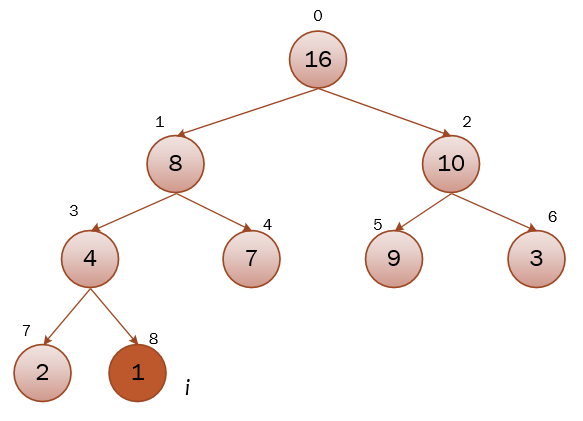
可以看到，在经历两次递归调用，逐级下沉，原来因为1节点变小，而被打破的最大堆，又重新维护完成。

2.建立最大堆 
我们采用自底向上的方法来建立一个最大堆。通过观察发现，下标为a.length / 2 到a.length - 1的节点均为叶子节点，没有子孩子。这意味着，它们已经是一个最大堆，只是仅有一个元素。因此，我们只需要自底向上，对其他节点调用maxHeapify来维护最大堆即可：

privatevoidbuildMaxHeap(int a[]) {        for (int i = a.length / 2 + 1; i >= 0; i--) {            maxHeapify(a, i);        }    }

注意，循环变量从a.length / 2 + 1开始，因为a.length / 2 到a.length - 1的节点满足最大堆，即a.length / 2 + 1的左右子孩子（如果有的话）是最大堆，符合使用maxHeapify调用条件。如果我们对数组[10, 8, 11, 8, 14, 9, 4, 1, 17]进行建立最大堆，那么输出数组为[17, 14, 11, 8, 10, 9, 4, 1, 8]: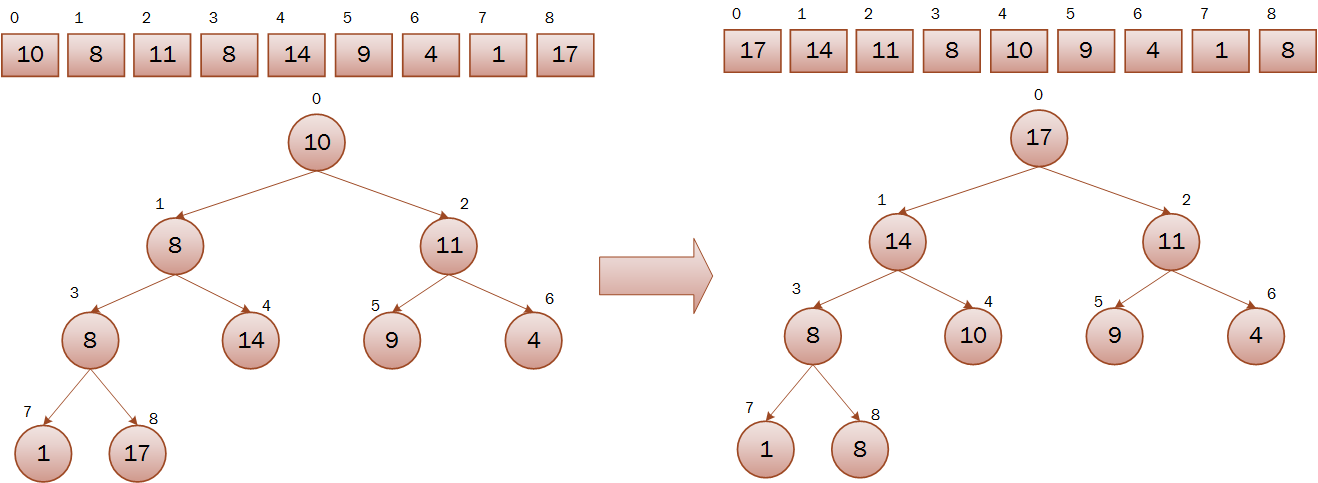 

3.堆排序 
在第二步建立完成最大堆之后，注意到整个数组的 最大元素 总是在最大堆的第一个，即a[0]。这时，如果我们拿走第一个元素，放到数组的最后一个位置，然后对第一个元素进行维护最大堆maxHeapify，如此循环进行，便可完成整个数组的排序。

    public void heapSort(int[] a) {        buildMaxHeap(a);//首先建立最大堆，完成后第一个元素为最大值intlength = a.length;        for (int i = a.length - 1; i >= 1; i--) {            swap(a, i, 0);//将第一个最大的元素移到后面，并且在maxHeapify的过程中通过减小length忽略它length--;&nb